|
В вопросах статики более жесткой средой естественно называть среду с меньшей сжимаемостью. Поведение таких сред ближе к поведению абсолютно жесткого тела, чем поведение сред с большей сжимаемостью. В акустике сжимаемость еще не определяет того, ведет ли себя данная среда по отношению к падающей на нее волне как податливая или как жесткая граница. В акустике следует сравнивать волновые сопротивления сред, т. е. отношения плотности к сжимаемости: та из двух сред жестче, для которой это ношение больше. Это обстоятельство снова подчеркивает своеобразие волновых задач сравнительно с задачами механики тел.
Меняя местами рс и р'с', найдем коэффициенты отражения и прохождения и для волны, падающей из второй среды на границу с первой: абсолютная величина коэффициента отражения будет та же, что и при падении из первой среды, но знак его изменится на обратный. Коэффициент прохождения изменится в отношении волновых сопротивлений сред. По абсолютной величине коэффициент отражения всегда меньше единицы (что следует и прямо из закона сохранения энергии); он положителен, если волна падает из среды с меньшим волновым сопротивлением, и отрицателен в обратном случае. Коэффициент прохождения всегда положителен и не превосходит 2.
Таким образом, отраженная и прошедшая волны равны: 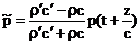 , , 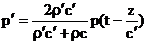 . .
Давление и скорость на границе (безразлично, с какой стороны от границы) равны:
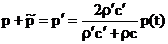 , , 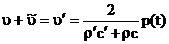 . (7) . (7)
Отношение давления к скорости частиц на границе оказывается равным волновому сопротивлению второй среды р'с'. Это можно было предвидеть, и не делая расчета, поскольку во второй среде имеется только бегущая волна.
Из формул Френеля видно, что коэффициенты отражения и прохождения зависят не от самих значений волнового сопротивления сред, а от их отношения. Отношение 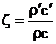 волновых сопротивлений первой и второй среды называют относительным волновым сопротивлением. Формулы Френеля выражаются через относительное волновое сопротивление следующим образом: волновых сопротивлений первой и второй среды называют относительным волновым сопротивлением. Формулы Френеля выражаются через относительное волновое сопротивление следующим образом:
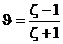 , , 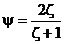 (8) (8)
Очевидно, 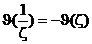 , ,
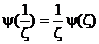 . .
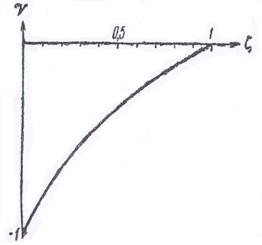
Рис. 1. Зависимость коэффициента отражения от относительного волнового сопротивления сред ζ. Для ζ>1 следует снять с графика значение 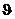 для 1/ζ и считать коэффициент отражения положительным. для 1/ζ и считать коэффициент отражения положительным.
На рис. 1 дан график зависимости коэффициента отражения от ζ. Согласно последним формулам можно обойтись участком графика для ζ<1 (где 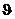 <0). Значения коэффициента прохождения получаются прибавлением единицы к коэффициенту отражения. При ζ=1. коэффициент отражения равен нулю и волна, нормально падающая на границу раздела двух сред, проходит из первой среды во вторую целиком, не отражаясь. Картина в первой среде в этом случае такая, как если бы волна полностью поглощалась границей. В этом случае достаточно возникновения только одной волны (прошедшей), чтобы, совместно с падающей, удовлетворить обоим граничным условиям. При ζ>1 коэффициент отражения положителен и при 殥 стремится к единице. <0). Значения коэффициента прохождения получаются прибавлением единицы к коэффициенту отражения. При ζ=1. коэффициент отражения равен нулю и волна, нормально падающая на границу раздела двух сред, проходит из первой среды во вторую целиком, не отражаясь. Картина в первой среде в этом случае такая, как если бы волна полностью поглощалась границей. В этом случае достаточно возникновения только одной волны (прошедшей), чтобы, совместно с падающей, удовлетворить обоим граничным условиям. При ζ>1 коэффициент отражения положителен и при 殥 стремится к единице.
Значения поля на границе, отнесенные к полю в падающей волне, равны 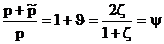 , , 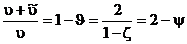 . .
Эти величины всегда положительны, и их полусумма равна единице. При ζ очень малом (вторая среда акустически очень мягкая по сравнению с первой, как, например, при отражении подводного звука от поверхности моря) давление стремится к нулю, а скорость частиц стремится к удвоенной скорости в падающей в падающей волне. При ζ очень большом (например, отражение воздушного звука от поверхности моря) к нулю стремится скорость частиц на границе, а удваивается давление. Предельный переход ζ к нулю и к бесконечности соответствует переходу к абсолютно мягкой и абсолютно жесткой границе.
Для иллюстрации сказанного приведем реальные (округленные) соотношения для прохождения звука из воздуха в воду и обратно при нормальном падении плоской волны. Для воды ρ=1 г/см3 ,с»1,5·105 см/сек (морская вода), rс=1,5·105 г/см2×сек; для воздуха r=0,00125 г/см3, с=3,4×104 см/сек, rс=42 г/см2×сек. При падении звука из воздуха в воду ζ=3500, 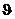 =0,99943, =0,99943, 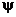 =1,99943, p¢/p=1,99943, =1,99943, p¢/p=1,99943, 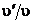 =0,00057. При падении звука из воды в воздух ζ=0,000285, =0,00057. При падении звука из воды в воздух ζ=0,000285, 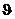 =—0,99943, =—0,99943, 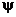 =0,00057, p¢/p=0,00057, =0,00057, p¢/p=0,00057, 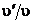 =1,99943. Отношение же потока энергии, проходящей через границу раздела, к потоку энергии в падающей волне составляет в обоих случаях 0,00114. =1,99943. Отношение же потока энергии, проходящей через границу раздела, к потоку энергии в падающей волне составляет в обоих случаях 0,00114.
Перейти на страницу: 1 2 3 |