|
Пусть плоская волна 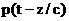 падает нормально на плоскую границу z=0 между двумя однородными средами. В первой среде возникает отраженная волна падает нормально на плоскую границу z=0 между двумя однородными средами. В первой среде возникает отраженная волна 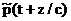 , а во второй — прошедшая , а во второй — прошедшая 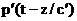 . .
Мы увидим сейчас, непосредственно произведя расчет, что отражение и прохождение всегда правильные. Отраженную и прошедшую волны можно записать в виде 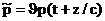 , , 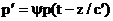 , ,
где 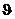 и и 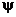 определяются свойствами сред и не зависят от формы волны. Для гармонических волн падающую, отраженную и прошедшую волны можно записать в виде определяются свойствами сред и не зависят от формы волны. Для гармонических волн падающую, отраженную и прошедшую волны можно записать в виде 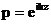 , , 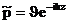 , , 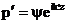 . .
Величины коэффициента отражения 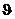 и коэффициента прохождения и коэффициента прохождения 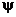 нужно подобрать так, чтобы были удовлетворены граничные условия. Граничных условий два: равенство давлений и равенство скоростей частиц по обе стороны границы. Со стороны первой среды берется суммарное поле падающей и отраженной волны, со стороны второй — поле прошедшей волны. нужно подобрать так, чтобы были удовлетворены граничные условия. Граничных условий два: равенство давлений и равенство скоростей частиц по обе стороны границы. Со стороны первой среды берется суммарное поле падающей и отраженной волны, со стороны второй — поле прошедшей волны.
Условие равенства давлений по обе стороны границы, или, что то же, непрерывность давления при переходе через границу, реально выполняется всегда. Нарушение этого условия вызвало бы бесконечное ускорение границы, так как сколь угодно тонкий слой сколь угодно малой массы, включающий внутри себя границу, находился бы тогда под действием конечной разности давлений по обеим сторонам слоя. В результате разность давлений выровнялась бы мгновенно.
Условие равенства скоростей выражает неразрывность среды на границе: среды не должны отдаляться друг от друга или проникать взаимно друг в друга. Это требование может на практике оказаться нарушенным, например, при кавитации, когда внутри жидкости образуются разрывы (разрывы возникают легче на границе двух сред, чем внутри одной среды). Будем считать, что нарушения граничных условий не происходит. В противном случае нижеследующий расчет неприменим, а отражение и прохождение окажутся неправильными.
Скорости частиц в падающей, отраженной и прошедшей волнах даются формулами 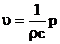 , , 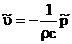 , , 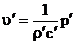 . .
Граничные условия можно написать так: при 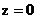 , , 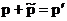 , , 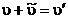 . .
Подставляя сюда соответственные выражения для давлений и скоростей частиц, найдем, сокращая на p(t):
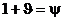 , , 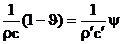 (5) (5)
Число граничных условий равно числу возникающих (помимо падающей) волн — отраженной и прошедшей, так что, подбирая соответственным образом оставшиеся пока неопределенными множители 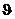 и и 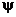 , всегда можно удовлетворить обоим граничным условиям, причем единственным образом. И это правило общее. В других акустических задачах число граничных условий может оказаться другим. Тогда возникнет и другое число волн, но оно снова равно числу граничных условий. , всегда можно удовлетворить обоим граничным условиям, причем единственным образом. И это правило общее. В других акустических задачах число граничных условий может оказаться другим. Тогда возникнет и другое число волн, но оно снова равно числу граничных условий.
В исключительных случаях удается удовлетворить граничным условиям меньшим числом волн (например, коэффициент отражения может обратиться в нуль), но никогда не бывает, чтобы при данном числе граничных условий падающая волна вызывала бы возникновение большего числа различных волн: так как равным числом волн уже можно удовлетворять граничным условиям, то получилось бы, что при одной и той же падающей волне и одних тех же препятствиях могут возникнуть различные волновые поля, а это противоречит принципу причинности.
Система (5) имеет единственное решение:
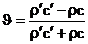 , , 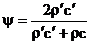 . (6) . (6)
Это — так называемые формулы Френеля (для нормального падения). Мы видим, что коэффициенты отражения и прохождения зависят только от волновых сопротивлений сред, и если эти сопротивления равны для обеих сред, то для нормального падения плоской волны среды акустически неразличимы: отражение от границы отсутствует и волна проходит во вторую среду целиком, как если бы все пространство было заполнено только первой средой. Для такого полного прохождения вовсе не требуется, чтобы плотности обеих сред и скорости звука в них равнялись друг другу в отдельности, т. е. чтобы совпадали механические свойства сред: достаточно равенства произведений плотности на скорость звука.
Перейти на страницу: 1 2 3 |