|
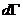 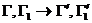 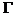 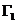 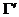 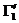 Во время столкновения молекул происходит изменение величин, от которых зависит функция распределения. Учитывая тот факт, что время наблюдения состояния системы и координаты частиц изменяются, не зависимо от того, произошло или нет столкновение частиц (которое влияет лишь на характер изменения координат),можно утверждать,что изменяются величины Г столкнувшихся молекул. Рассматривая достаточно малый интервал, обнаружим, что молекулы при столкновении выводятся из этого интервала, т.е. имеют место акты “ухода”. Пусть двум столкнувшимся молекулам соответствуют, как и ранее, величины и до столкновения ,а , после столкновения (для краткости говорим о переходе ). Во время столкновения молекул происходит изменение величин, от которых зависит функция распределения. Учитывая тот факт, что время наблюдения состояния системы и координаты частиц изменяются, не зависимо от того, произошло или нет столкновение частиц (которое влияет лишь на характер изменения координат),можно утверждать,что изменяются величины Г столкнувшихся молекул. Рассматривая достаточно малый интервал, обнаружим, что молекулы при столкновении выводятся из этого интервала, т.е. имеют место акты “ухода”. Пусть двум столкнувшимся молекулам соответствуют, как и ранее, величины и до столкновения ,а , после столкновения (для краткости говорим о переходе ).
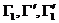 Полное число столкновений при вышеуказанном переходе со всеми возможными значениями Полное число столкновений при вышеуказанном переходе со всеми возможными значениями
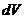 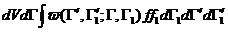 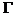 при заданном , происходящих в единицу времени в объёме ,определяется интегралом при заданном , происходящих в единицу времени в объёме ,определяется интегралом
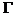 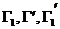 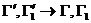 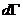 В то же время происходят столкновения иного рода (называемые “приходом”), в результате которых молекулы, обладавшие до столкновения значениями величин , лежащими вне заданного интервала , попадают в этот интервал. Такие переходы могут быть обозначены следующим образом: (со всеми возможными значениями при заданном ). Аналогично первому типу перехода полное число таких столкновений в единицу времени в объёме равно: В то же время происходят столкновения иного рода (называемые “приходом”), в результате которых молекулы, обладавшие до столкновения значениями величин , лежащими вне заданного интервала , попадают в этот интервал. Такие переходы могут быть обозначены следующим образом: (со всеми возможными значениями при заданном ). Аналогично первому типу перехода полное число таких столкновений в единицу времени в объёме равно:
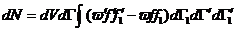 В результате всех столкновений изменение числа молекул в единицу времени в элементарном объёме определяется разностью между числом актов ухода и числом актов прихода: В результате всех столкновений изменение числа молекул в единицу времени в элементарном объёме определяется разностью между числом актов ухода и числом актов прихода:
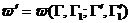 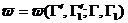 (9) , где (9) , где
и
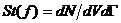 Интеграл столкновений может быть определён как: Интеграл столкновений может быть определён как:
(10)
(изменение числа частиц в единицу времени в фазовом объёме dVdГ )
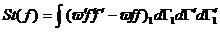 Из соотношений (8) и (9) получим вид интеграла столкновений Из соотношений (8) и (9) получим вид интеграла столкновений
(11)
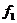 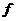 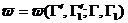 Заметим, что во втором члене подынтегрального выражения интегрирование по имеет Заметим, что во втором члене подынтегрального выражения интегрирование по имеет
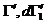 отношение только к функции . Множители и не зависят от переменных . Преобразовав эту часть интеграла с помощью соотношения (4) , получим окончательный вид интеграла столкновений отношение только к функции . Множители и не зависят от переменных . Преобразовав эту часть интеграла с помощью соотношения (4) , получим окончательный вид интеграла столкновений
|