|
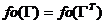 (2) (2)
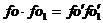 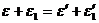 V – макроскопическая скорость движения газа как целого. В силу закона сохранения энергии при столкновении двух молекул . Поэтому можно записать (3) V – макроскопическая скорость движения газа как целого. В силу закона сохранения энергии при столкновении двух молекул . Поэтому можно записать (3)
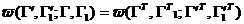 Отметим ещё тот факт, что сама функция вероятности в принципе может быть определена лишь путём решения механической задачи о столкновении частиц. Написанное выше равенства (1) , (2) и (3) дадут после сокращений в (1) Отметим ещё тот факт, что сама функция вероятности в принципе может быть определена лишь путём решения механической задачи о столкновении частиц. Написанное выше равенства (1) , (2) и (3) дадут после сокращений в (1)

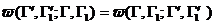 С учётом утверждения (*) С учётом утверждения (*)
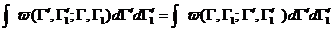 Интегрируя последнее равенство (для использования в дальнейшем) получаем соотношение: Интегрируя последнее равенство (для использования в дальнейшем) получаем соотношение:
(4)
§3 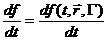 Вывод кинетического уравнения. Вывод кинетического уравнения.
Рассмотрим производную от функции распределения по времени:
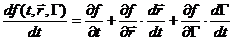 При движении молекул газа в отсутствии внешнего поля величины Г, как интегралы движения, не изменяются. При движении молекул газа в отсутствии внешнего поля величины Г, как интегралы движения, не изменяются.
(5)
(последнее слагаемое в выражении производной обнуляется , т.к. )
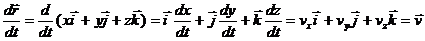
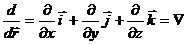 ( оператор набла) ( оператор набла)
Выражение для производной примет вид : (6)
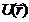 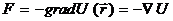 Пусть теперь газ находится во внешнем потенциальном поле , действующем на координаты центра тяжести молекул (например, в гравитационном поле). И пусть F – сила, действующая со стороны поля на частицу. Пусть теперь газ находится во внешнем потенциальном поле , действующем на координаты центра тяжести молекул (например, в гравитационном поле). И пусть F – сила, действующая со стороны поля на частицу.
(7)
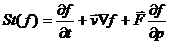
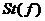 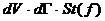 Правую часть равенства (6) обозначим через . Символ означает Правую часть равенства (6) обозначим через . Символ означает
скорость изменения функции распределения благодаря столкновениям, а величина
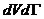 есть отнесённое к единице времени изменение за счёт столкновений числа молекул в фазовом объёме . Полное изменение функции распределения в заданной точке фазового пространства запишется в виде : есть отнесённое к единице времени изменение за счёт столкновений числа молекул в фазовом объёме . Полное изменение функции распределения в заданной точке фазового пространства запишется в виде :
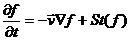 (8) (8)
Перейти на страницу: 1 2 3 |