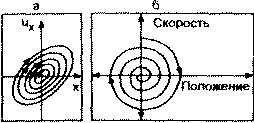
Рис 178 Фазовая траектория маятника а - без затухания, б-с затуханием

Эволюцию динамических систем во времени оказалось удобным анализировать с помощью фазового пространства - абстрактного пространства с числом измерений, равным числу переменных, характеризующих состояние системы Примером может служить пространство, имеющее в качестве своих координат координаты и скорости всех частиц системы Для линейного гармонического осциллятора (одна степень свободы) размерность фазового пространства равна двум (координата и скорость

колеблющейся частицы) Такое фазовое пространство есть плоскость, эволюция системы соответствует непрерывному изменению координаты и скорости, и точка, изображающая состояние системы, движется по фазовой траектории (рис 178) Фазовые траектории такого маятника (линейного гармонического осциллятора), который колеблется без затухания, представляют собой эллипсы

(mv2^) + (mo)^/2) x2 = const

В случае затухания фазовые траектории при любых начальных значениях оканчиваются в одной точке, которая соответствует покою в положении равновесия и точка, или аттрактор, как бы притягивает к себе со временем все фазовые траектории (англ to attract "притягивать") и является обобщением понятия равновесия, состояние, которое притягивает системы Маятник из-за трения сначала замедляет колебания, а затем останавливается На диаграмме его состоянии (фазовой диаграмме) по одной оси откладывают угол отклонения маятника от вертикали, а по другой - скорость изменения этого угла Получается фазовый портрет в виде точки, движущейся вокруг начала отсчета Начало отсчета и будет аттрактором, поскольку как бы притягивает точку, представляющую движение маятника по фазовой диаграмме В таком простом аттракторе нет ничего странного

В более сложных движениях, например, маятника часов с грузом на цепочке, груз играет роль механизма, подкачивающего энергию к маятнику, и маятник не замедляет колебаний Если запустить часы энергичным толчком маятника, он замедлится до темпа, который обусловлен весом груза, после чего характер его движения останется неизменным Если толчок будет слабым, маятник, замедляясь, вскоре остановится Ситуации с сильным начальным толчком на фазовой диаграмме соответствует спираль, обвивающаяся все более плотно вокруг круговой орбиты, аттрактор будет в данном случае окружностью, т.е. объектом не более странным, чем точка Разным маятникам соответствуют аттракторы, которые называют предельными циклами Все фазовые траектории, соответствующие разным начальным условиям, выходят на периодическую траекторию, которая отвечает установившемуся движению если начальные отклонения были малыми, они возрастут, а, если амплитуды были большими, то уменьшатся. Биение сердца тоже изображается предельным циклом - установившимся режимом.

Если движение состоит из наложения двух колебаний разных частот, то фазовая траектория навивается на тор в фазовом пространстве трех измерений. Это движение устойчиво, а две фазовые траектории, начинающиеся рядом, будут навиваться на тор, не уходя друг от друга. Ситуация соответствует устойчивому установившемуся движению, к которому сама стремится.