|
Рассмотрим простые физические модели диспергирующих сред. Ясно, что простые модели, отражающие реальные свойства среды, могут быть построены в немногих случаях. Тем не менее они очень важны для понимания физики и заслуживают подробного обсуждения.
Для нахождения зависимости 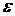 от частоты (закона дисперсии) необходимо решить задачу о взаимодействии электромагнитной волны с имеющимися в среде зарядами. от частоты (закона дисперсии) необходимо решить задачу о взаимодействии электромагнитной волны с имеющимися в среде зарядами.
Все современные теории дисперсии учитывают молекулярное строение вещества и рассматривают молекулы как динамические системы, обладающие собственными частотами. Молекулярные системы подчиняются законам квантовой механики. Однако результаты классической теории дисперсии во многих случаях приводят к качественно правильному выражению для показателей преломления и поглощения как функций частоты.
Диэлектрики условно разделяются на два типа — неполярные и полярные. В молекулах неполярных диэлектриков заряды электронов точно компенсируют заряды ядер, причем центры отрицательных и положительных зарядов совпадают. В этом случае в отсутствие электромагнитного поля молекулы не обладают дипольным моментом. Под действием поля волны происходит смещение электронов (ионы при этом можно считать неподвижными, поскольку их масса велика по сравнению с массой электронов) а каждая молекула поляризуется — приобретает дипольный момент 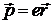 . Если диэлектрик однороден и в единице объема содержится . Если диэлектрик однороден и в единице объема содержится 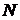 одинаковых молекул, то вектор объемной плотности поляризации одинаковых молекул, то вектор объемной плотности поляризации 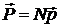 . .
Для определения вектора 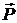 необходимо решить уравнение движения электронов в молекуле под действием поля волны и найти смещение электронов как функцию поля. В классической теории дисперсии описание движения электронов в молекуле основано на модели Друде — Лоренца, согласно которой молекула представляется в виде одного или нескольких линейных гармонических осцилляторов, соответствующих нормальным колебаниям электронов в молекуле. Рассмотрим уравнение движения такого осциллятора: необходимо решить уравнение движения электронов в молекуле под действием поля волны и найти смещение электронов как функцию поля. В классической теории дисперсии описание движения электронов в молекуле основано на модели Друде — Лоренца, согласно которой молекула представляется в виде одного или нескольких линейных гармонических осцилляторов, соответствующих нормальным колебаниям электронов в молекуле. Рассмотрим уравнение движения такого осциллятора:
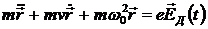 . (2.1) . (2.1)
Здесь 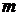 — эффективная масса, — эффективная масса, 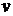 — константа затухания, имеющая размерность частоты, — константа затухания, имеющая размерность частоты, 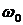 — резонансная угловая частота нормального колебания, — резонансная угловая частота нормального колебания, 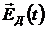 — поле, действующее на диполь. Для плотных сред действующее поле — поле, действующее на диполь. Для плотных сред действующее поле 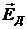 в однородном диэлектрике отличается от среднего макроскопического поля в среде на величину в однородном диэлектрике отличается от среднего макроскопического поля в среде на величину 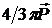 и равно и равно
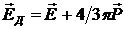 . .
Отметим, что последнее равенство справедливо для изотропной среды и для кристаллов кубической симметрии.
При гармонической зависимости от времени поля 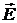 из уравнения (2.1) получим следующее соотношение: из уравнения (2.1) получим следующее соотношение:
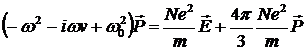 . .
Отсюда удобно выразить 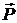 : :
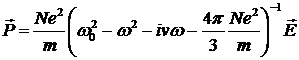 . (2.2) . (2.2)
Учитывая, что 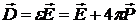 , из (2.2) найдем , из (2.2) найдем
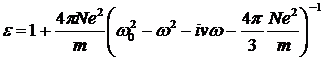 , (2.3) , (2.3)
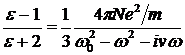 . .
Разделяя в (2.3) действительную и мнимую части, получим
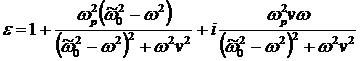 . .
Здесь введены обозначения 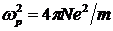 , , 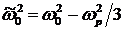 . В случае низких частот, удовлетворяющих условию . В случае низких частот, удовлетворяющих условию 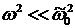 , придем к выражению для статической диэлектрической проницаемости , придем к выражению для статической диэлектрической проницаемости
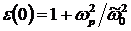 . .
Для твердых и жидких диэлектриков 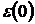 может значительно превышать единицу. может значительно превышать единицу.
В газах плотность поляризованных молекул обычно невелика. При этом 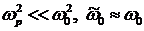 и можно считать, что и можно считать, что 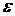 мало отличается от единицы. Поэтому мало отличается от единицы. Поэтому
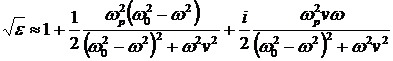 . (2.4) . (2.4)
|