|
Обозначим плотности и медленности звука в, первой и второй среде соответственно через r, r' и S, S' и рассмотрим падение на границу волны вида 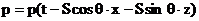 . .
Если отражение правильное, то, как уже было сказано, отраженную и прошедшую волны можно записать в виде 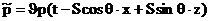 , ,
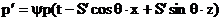 . .
Например, для падающей гармонической волны 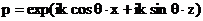
отраженная и прошедшая волны равны 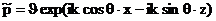 , ,
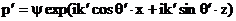 . .
В написанных выше формулах величины 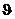 и и 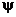 — неизвестные пока коэффициенты отражения и прохождения, которые должны быть определены из граничных условий. — неизвестные пока коэффициенты отражения и прохождения, которые должны быть определены из граничных условий.
Граничные условия — это равенство давлений и нормальных скоростей частиц по обе стороны границы раздела сред. На касательные компоненты скорости никаких ограничений в идеальных средах не накладывается: в решении, которое мы найдем, эти компоненты окажутся различными. Получающийся разрыв касательной компоненты скорости частиц на границе совместим с принятым предположением об идеальности среды, т. е. об отсутствии вязкости. Для реальных жидкостей разрыв сглаживают вязкие волны. Обычно они мало влияют на картину отражения и прохождения; поэтому мы пока пренебрежем ими, считая жидкость идеальной.
Так как на границе аргументы функции ρ одинаковы для всех трех волн, то граничные условия можно записать для волны любой формы в виде
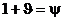 , , 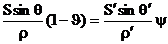 . (9) . (9)
Первое уравнение совпадает с соответственным уравнением для нормального падения (первое уравнение (5)). Это объясняется тем, что давление — скаляр, и поэтому условие, на него налагаемое, не связано с направлением распространения волн. Второе уравнение иное, чем для нормального падения: в него входят нормальные компоненты векторов скорости частиц, которые зависят не только от величины, но и от направления этих векторов.
Решая уравнения (9) относительно коэффициентов отражения и прохождения, найдем
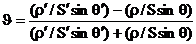 , , 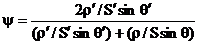 (10) (10)
или, через волновое сопротивления
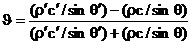 , , 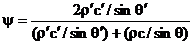 . (11) . (11)
В отличие от случая нормального падения, коэффициенты оказались зависящими не только от свойств самих сред, но и от угла скольжения падающей волны. В частности, при одинаковых волновых сопротивлениях обеих сред, но неравных плотностях и скоростях звука в отдельности, коэффициент отражения не равен нулю.
Пользуясь принятыми ранее обозначениями, можем переписать формулы (10) в таком виде:
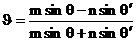 , , 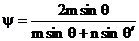 . (12) . (12)
Из этих формул можно исключить угол скольжения преломленной волны:
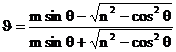 , , 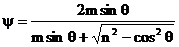 . (13) . (13)
Наконец, деля числитель и знаменатель на sinθ, получим формулы, куда входит только одна тригонометрическая функция:
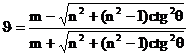 , , 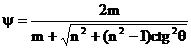 . (14) . (14)
Полученные выражения для 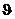 и и 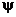 — формулы Френеля для наклонного падения. — формулы Френеля для наклонного падения.
В различных задачах удобно пользоваться то одним, то другим представлением этих коэффициентов.
|