|
Для проводящей среды в асимптотике металлов (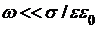 ), как показал анализ [7], распространение волн всех четырех электродинамических составляющих реального электромагнитного поля подчиняется теоретически хорошо изученному закону для плоских волн ЭМ поля в металлах [1], где все волновые решения имеют вид экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами на ), как показал анализ [7], распространение волн всех четырех электродинамических составляющих реального электромагнитного поля подчиняется теоретически хорошо изученному закону для плоских волн ЭМ поля в металлах [1], где все волновые решения имеют вид экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами на 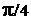 . .
Однако вернемся к анализу энергетики распространения составляющих реального электромагнитного поля в виде плоских волн в диэлектрической среде без потерь (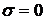 ). Вначале обратимся к закону сохранения электрической энергии, соотношение которого согласно (10) запишется как: ). Вначале обратимся к закону сохранения электрической энергии, соотношение которого согласно (10) запишется как:
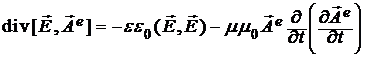
.
(12)
Выясним, выполняется ли это выражение для плоской монохроматической электрической волны, полевые компоненты которой, согласно волновым решениям уравнений системы (7), обладая сдвигом фазы на 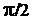 , имеют следующий вид: , имеют следующий вид: 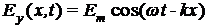 и и 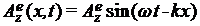 . Тогда, подставляя их в соотношение (12), приходим к соотношению: . Тогда, подставляя их в соотношение (12), приходим к соотношению:
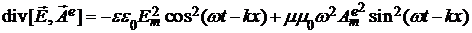
.
Такой результат вполне удовлетворяет закону сохранения энергии, поскольку усреднение по времени этого соотношения дает
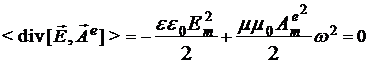
, (13)
а потому электрическая волна действительно переносит в пространстве чисто электрическую энергию: 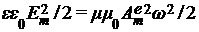 , не зависящую от времени и точек пространства. , не зависящую от времени и точек пространства.
Соответственно, для магнитного поля, распространяющегося в однородной среде без потерь, закон сохранения магнитной энергии согласно (11) запишется в виде соотношения:
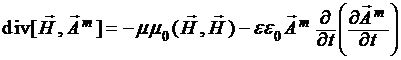
.
(14)
Рассмотрим, как выполняется этот закон для плоской монохроматической магнитной волны, полевые компоненты которой, согласно волновым решениям уравнений (8), имеют следующий вид: 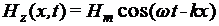 и и 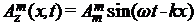 . Подставляя их в соотношение (14) и проводя аналогичные рассуждения как при выводе формулы (13), получаем в итоге: . Подставляя их в соотношение (14) и проводя аналогичные рассуждения как при выводе формулы (13), получаем в итоге:
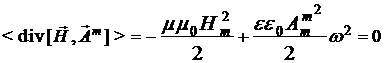
. (15)
Итак, в случае магнитного поля снова приходим к физически здравому результату, когда в пространстве без потерь посредством магнитной волны переносится чисто магнитная энергия 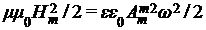 , не зависящая от времени и точек пространства. Следовательно, распространение магнитной волны также удовлетворяет закону сохранения энергии. , не зависящая от времени и точек пространства. Следовательно, распространение магнитной волны также удовлетворяет закону сохранения энергии.
Таким образом, аргументированно установлено, что в Природе объективно существует сравнительно сложное и необычное с точки зрения традиционных представлений вихревое четырехвекторное поле в виде совокупности функционально связанных между собой четырех вихрево-полевых компонент 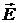 , , 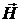 и и 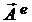 , ,
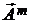 . Это поле, условно названное реальным электромагнитным полем . Это поле, условно названное реальным электромагнитным полем
, реализуется четверкой составляющих его электродинамических полей, состоящих из пар вышеуказанных компонент: электрическое поле с 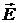 и и 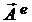 , магнитное поле с , магнитное поле с 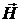 и и 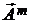 , электромагнитное поле с , электромагнитное поле с 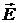 и и 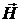 , наконец, поле векторного потенциала с , наконец, поле векторного потенциала с 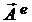 и и 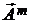 . Причем способностью к непосредственному распространению в пространстве в виде волн, отвечающих обычным физическим представлениям о волновом процессе, обладают только электрическое и магнитное поля за счет наличия у этих волн сдвига фазы на . Причем способностью к непосредственному распространению в пространстве в виде волн, отвечающих обычным физическим представлениям о волновом процессе, обладают только электрическое и магнитное поля за счет наличия у этих волн сдвига фазы на 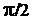 между их компонентами между их компонентами 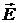 и и 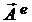 , соответственно, , соответственно, 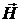 и и 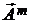 . Реализация же собственно волн ЭМ поля и ЭМ векторного потенциала невозможна в принципе, хотя сами эти поля, как показано выше, существуют и распространяются опосредованно в виде псевдоволн, поскольку их синфазные компоненты являются составной частью компонент электрической и магнитной волн, распространяющихся обычным образом. Именно тем самым все составляющие реального электромагнитного поля . Реализация же собственно волн ЭМ поля и ЭМ векторного потенциала невозможна в принципе, хотя сами эти поля, как показано выше, существуют и распространяются опосредованно в виде псевдоволн, поскольку их синфазные компоненты являются составной частью компонент электрической и магнитной волн, распространяющихся обычным образом. Именно тем самым все составляющие реального электромагнитного поля
Перейти на страницу: 2 3 4 5 6 7 8 |